Cymatics – The Science of the Future
By Peter Pettersson, translation Yarrow Cleaves
In this article we will see what various researchers in this field, which has been given the name of Cymatics, have concluded.
– Is there a connection between sound, vibrations and physical reality?
– Do sound and vibrations have the potential to create?
What is a Cymatic water-sound-motion?
Water in a round cup, that is oscillating up and down with a certain frequency, will react on this impulse with waves on her surface. The water oscillates up and down in the middle, like when a stone is thrown in a pool. Like there a ringwave will grow out, and is been followed by other circular waves, all with the same centre, so concentric.
Ernst Chladni
In 1787, the jurist, musician and physicist Ernst Chladni published Entdeckungen über die Theorie des Klangesor ( Discoveries Concerning the Theory of Sound). In this and other pioneering works, Chladni, who was born in 1756, the same year as Mozart, and died in 1829, the same year as Beethoven, laid the foundations for that discipline within physics that came to be called acoustics, the science of sound. Among Chladni´s successes was finding a way to make visible what sound waves generate. With the help of a violin bow which he drew perpendicularly across the edge of flat plates covered with sand, he produced those patterns and shapes which today go by the term Chladni figures. What was the significance of this discovery? Chladni demonstrated once and for all that sound actually does affect physical matter and that it has the quality of creating geometric patterns.
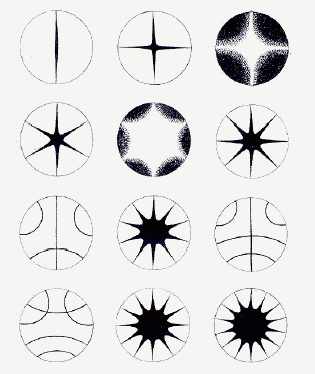
Chladni figures.
What we are seeing in this illustration is primarily two things: areas that are and are not vibrating. When a flat plate of an elastic material is vibrated, the plate oscillates not only as a whole but also as parts. The boundaries between these vibrating parts, which are specific for every particular case, are called node lines and do not vibrate. The other parts are oscillating constantly. If sand is then put on this vibrating plate, the sand (black in the illustration) collects on the non-vibrating node lines. The oscillating parts or areas thus become empty. According to Jenny, the converse is true for liquids; that is to say, water lies on the vibrating parts and not on the node lines.
Lissajous Figures
In 1815 the American mathematician Nathaniel Bowditch began studying the patterns created by the intersection of two sine curves whose axes are perpendicular to each other, sometimes called Bowditch curves but more often Lissajous figures (see left and below images).
 |
This after the French mathematician Jules-Antoine Lissajous, who, independently of Bowditch, investigated them in 1857-58. Both concluded that the condition for these designs to arise was that the frequencies, or oscillations per second, of both curves stood in simple whole-number ratios to each other, such as 1:1, 1:2, 1:3, and so on. In fact, one can produce Lissajous figures even if the frequencies are not in perfect whole-number ratios to each other. If the difference is insignificant, the phenomenon that arises is that the designs keep changing their appearance. They move. What creates the variations in the shapes of these designs is the phase differential, or the angle between the two curves. In other words, the way in which their rhythms or periods coincide. If, on the other hand, the curves have different frequencies and are out of phase with each other, intricate web-like designs arise. These Lissajous figures are all visual examples of waves that meet each other at right angles.
Lissajous figures. As I pondered the connection between these figures and other areas of knowledge, I came to think about the concept that exists in many societies and their mythologies around the world, which describes the world as a web. |
For example, many of the Mesoamerican people regarded the various parts of the universe as products of spinning and weaving: “Conception and birth were/…/ compared with the acts of spinning and weaving; all the Aztec and Mayan creation and fertility goddesses were described as great weavers.”(1) A number of waves crossing each other at right angles look like a woven pattern, and it is precisely that they meet at 90-degree angles that gives rise to Lissajous figures.
Hans Jenny
In 1967, the late Hans Jenny, a Swiss doctor, artist, and researcher, published the bilingual book Kymatik -Wellen und Schwingungen mit ihrer Struktur und Dynamik/ Cymatics – The Structure and Dynamics of Waves and Vibrations. In this book Jenny, like Chladni two hundred years earlier, showed what happens when one takes various materials like sand, spores, iron filings, water, and viscous substances, and places them on vibrating metal plates and membranes. What then appears are shapes and motion- patterns which vary from the nearly perfectly ordered and stationary to those that are turbulently developing, organic, and constantly in motion.
Jenny made use of crystal oscillators and an invention of his own by the name of the tonoscope to set these plates and membranes vibrating. This was a major step forward. The advantage with crystal oscillators is that one can determine exactly which frequency and amplitude/volume one wants. It was now possible to research and follow a continuous train of events in which one had the possibility of changing the frequency or the amplitude or both.
The tonoscope was constructed to make the human voice visible without any electronic apparatus as an intermediate link. This yielded the amazing possibility of being able to see the physical image of the vowel, tone or song a human being produced directly. (se below) Not only could you hear a melody – you could see it, too!
Jenny called this new area of research cymatics, which comes from the Greek kyma, wave. Cymatics could be translated as: the study of how vibrations, in the broad sense, generate and influence patterns, shapes and moving processes.
The Creative Vibration
What did Hans Jenny find in his investigations?
In the first place, Jenny produced both the Chladni figures and Lissajous figures in his experiments. He discovered also that if he vibrated a plate at a specific frequency and amplitude – vibration – the shapes and motion patterns characteristic of that vibration appeared in the material on the plate. If he changed the frequency or amplitude, the development and pattern were changed as well. He found that if he increased the frequency, the complexity of the patterns increased, the number of elements became greater. If on the other hand he increased the amplitude, the motions became all the more rapid and turbulent and could even create small eruptions, where the actual material was thrown up in the air.
The development of a pattern in sand (step by step).
Swinging water drops (by Hans Jenny)
Sand patterns as a function of the size of the plate
The shapes, figures and patterns of motion that appeared proved to be primarily a function of frequency, amplitude, and the inherent characteristics of the various materials. He also discovered that under certain conditions he could make the shapes change continuously, despite his having altered neither frequency nor amplitude!
The vowel A in sand
When Jenny experimented with fluids of various kinds he produced wave motions, spirals, and wave-like patterns in continuous circulation. In his research with plant spores, he found an enormous variety and complexity, but even so, there was a unity in the shapes and dynamic developments that arose. With the help of iron filings, mercury, viscous liquids, plastic-like substances and gases, he investigated the three-dimensional aspects of the effect of vibration.
In his research with the tonoscope, Jenny noticed that when the vowels of the ancient languages of Hebrew and Sanskrit were pronounced, the sand took the shape of the written symbols for these vowels, while our modern languages, on the other hand, did not generate the same result! How is this possible? Did the ancient Hebrews and Indians know this? Is there something to the concept of “sacred language,” which both of these are sometimes called? What qualities do these “sacred languages,” among which Tibetan, Egyptian and Chinese are often numbered, possess? Do they have the power to influence and transform physical reality, to create things through their inherent power, or, to take a concrete example, through the recitation or singing of sacred texts, to heal a person who has gone “out of tune”?
to read the rest of the article, for sources, etc., go to: http://blog.world-mysteries.com/science/cymatics/